How to prevent mass death

Posted on by

Disclaimer: As people have pointed out on reddit, a logistic curve is not a very good model for this. I will post an analysis with a better model as I learn more.

tl;dr: if we model Covid-19 growth as a logistic curve, then we need a doubling time of more than 124 days to avoid overwhelming hospitals in the US.

It is becoming clear that the danger from the SARS-CoV-II coronavirus is systemic healthcare failure. This is because the virus is growing exponentially. In the US, the doubling time seems to be about 2 days, which means that if your city has 10 cases, 2 days later it will have 20 cases, 4 days later it will have 40 cases, and 20 days later it will have 10,240 cases.

This growth, of course, will not continue unabated. When enough people have gotten the virus, the growth will start to slow, as many people will be immune. So a better approximation than an exponential is a logistic curve.

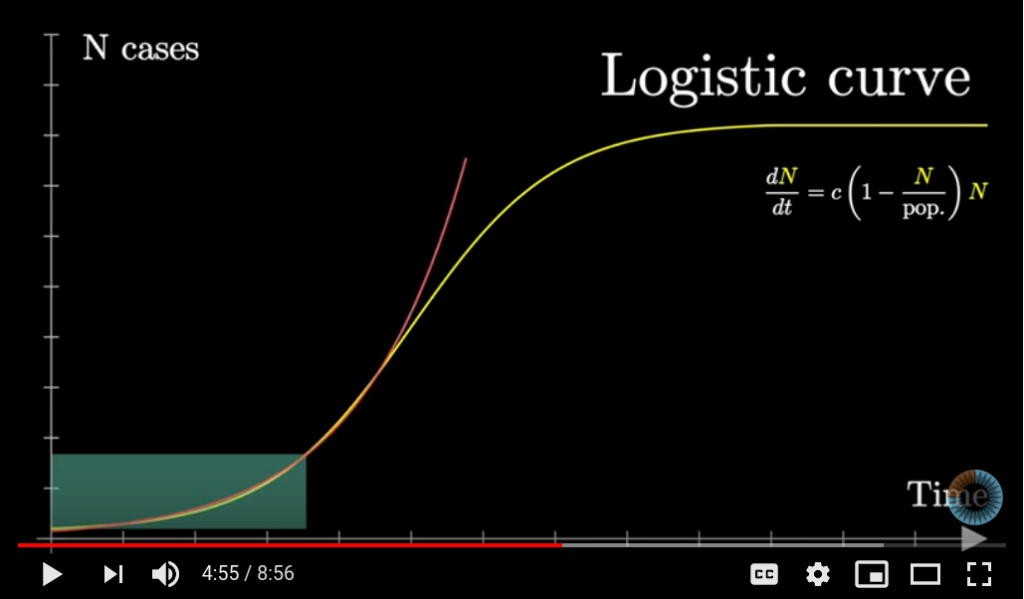
Source: 3Blue1Brown. Exponential curve in red, logistic curve in yellow.

Notice that the growth accelerates until the point of inflection, when exactly half of the population is infected, and then starts to slow down.

Let P be the population. I think it will be easier if we define n=N/P. Then dividing both sides of the pictured equation by P gives \frac{d}{dt}\frac{N}{P}=c(1-\frac{N}{P})\frac{N}{P}, or \frac{dn}{dt}=c(1-n)n, which is simpler and coincides with Wikipedia’s formula.

The pictured differential equation is actually an instance of the Law of Mass Action. People get infected when an infected person comes into contact with an susceptible person, so the rate of the reaction, i.e. the rate at which new people get infected, is proportional to (the number of infected people) times (the number of susceptible people). In other words, \frac{dn}{dt} is proportional to ns, where s is the proportion of the population that is susceptible to infection. We recover the above differential equation by assuming that all people who have not yet become infected are susceptible, i.e. s=1-n, and letting c be the constant of proportionality.

When n is very small, 1-n\approx 1 so our equation is approximately \frac{dn}{dt}=cn. The solution to this is an exponential: n(t)=Ae^{ct}. Thus we identify the constant c as the growth rate.

Assuming this model, we cannot prevent everyone from getting infected at some point. What we can change, through NPIs (non-pharmacological interventions like quarantines and shutdowns), is c, the growth rate. If c is too high, it will overwhelm hospitals.

The curve on the left is what will happen with a high c, the curve on the right is what will happen with a low c.

So how do we determine whether hospitals will be overwhelmed, given a certain value of c? We first need an estimate for how long patients will be in the hospital. A quick google search turns up a study saying that out of a certain sample in Jiangsu Province, the mean length of stay is 8 days.

This means that h(t), which we define as the proportion of the population who are in the hospital on day t, is, on average, equal to the proportion of people who were newly symptomatic in the last 10 days times the fraction of cases which have to be hospitalized, which is about 20\%. So we can approximate h(t) = 20\%(n(t)-n(t-10)), which in turn we can approximate as 20\%\cdot 10n'(t)=2n'(t).

The number of staffed beds in US hospitals is 924,107. The population of the US is 327.2 million. Thus there are 924,107/327,200,000 = 0.0028 staffed beds per capita, or 2.8 staffed beds per thousand people.

If we don’t want hospitals to be overwhelmed, then we can’t let h(t) get higher than 0.0028. What will h(t) be at it’s maximum? Well h(t)=2n'(t)=2cn(t)(1-n(t)). This quantity is maximized when n(t)=\frac{1}{2} (to see this, graph it, complete the square, or find a critical point). So at it’s maximum h(t)=2c\frac{1}{2}\frac{1}{2}=\frac{c}{2}. So to prevent hospitals being overwhelmed, we need to ensure that \frac{c}{2}\leq 0.0028, i.e. c\leq 0.0056.

To put this in more familiar terms, let’s express it in terms of the doubling time, the amount of time that it takes n to double in the early stages when it is growing exponentially. Call this doubling time T. Then e^{cT}=2, so T=\frac{\ln{2}}{c}. The condition c\leq 0.0056 is equivalent to the condition T\geq \frac{\ln{2}}{0.0056}=124.

So we need a doubling time of more than 124 days! Wow! That is difficult to imagine given that now the US has a doubling time of 2.15 days, and that China has the highest doubling time of any country at 29 days.

Perhaps if we slow it down now we could buy ourselves time to increase hospital capacity, so that the doubling time doesn’t have to be so high.

Or perhaps, I’m using an overly pessimistic model. Indeed, this model does assume that people who are infected are infectious forever after, and that all people who have not yet been infected are susceptible.

Leave a comment