So I just read the first chapter of John Stillwell’s Naive Lie Theory, and now I understand how quaternions can be used to represent spatial rotation! Previously, I could do the calculation but I didn’t understand why it was true. Here’s the way I understand it, which is inspired by but not identical to Stillwell. First of all, what exactly is the claim that I now understand?
A purely imaginary quaternion  can be thought of as a vector
can be thought of as a vector  in
in 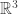 . Thus we can think of a general quaternion as the sum of a scalar and a vector:
. Thus we can think of a general quaternion as the sum of a scalar and a vector: 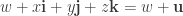 . Thus any unit quaternion can be written
. Thus any unit quaternion can be written  for some angle
for some angle  and unit vector
and unit vector 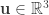 .
.
The claim concerns rotations in 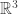 . Apparently, the rotation by the angle
. Apparently, the rotation by the angle  about the axis
about the axis  is represented by the unit quaternion
is represented by the unit quaternion  . To rotate a vector
. To rotate a vector  by this rotation, we write
by this rotation, we write 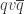 . People really like this because it makes 3D spatial rotation into quaternion multiplication, which is much easier and less messy than using
. People really like this because it makes 3D spatial rotation into quaternion multiplication, which is much easier and less messy than using 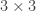 matrices. Computer graphics use quaternions for this reason. Also, this gives a nice interpretation for quaternions, which otheriwse have unclear meaning: rotations of
matrices. Computer graphics use quaternions for this reason. Also, this gives a nice interpretation for quaternions, which otheriwse have unclear meaning: rotations of 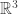 . Later in this post we will see an even nicer interpretation.
. Later in this post we will see an even nicer interpretation.
Now why does this work?
First let’s see what happens when two vectors (purely imaginary quaternions) are multiplied.

We can recognize the right-hand-side as minus the dot product plus the cross product of the two vectors:
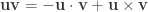
Two interesting special cases of this:
1) If 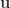 and
and 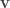 are parallel, then their cross product is
are parallel, then their cross product is  , so
, so 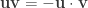 . In particular,
. In particular,  . If
. If 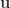 is a unit vector, then its square is
is a unit vector, then its square is 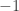 , just like
, just like 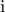 ,
, 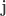 , and
, and  . This means that the set of quaternions
. This means that the set of quaternions  are a replica of the complex plane: they add and multiply just like complex numbers
are a replica of the complex plane: they add and multiply just like complex numbers  .
.
2) If 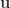 and
and 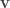 are orthogonal, then their dot product is
are orthogonal, then their dot product is  , so
, so  . In this case, let’s define
. In this case, let’s define  . Now the vectors
. Now the vectors 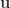 ,
, 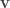 , and
, and 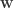 are mutually orthogonal. Let’s assume that
are mutually orthogonal. Let’s assume that 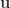 and
and 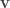 are both unit vectors, and see how
are both unit vectors, and see how 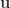 ,
, 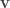 , and
, and 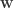 multiply:
multiply:
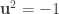 (by the first special case)
(by the first special case)

 (since
(since  is a unit vector)
is a unit vector)
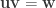
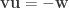 (because cross product is antisymmetric)
(because cross product is antisymmetric)
 (by previous line, associativity of quaternion multiplication,
(by previous line, associativity of quaternion multiplication,  )
)
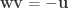
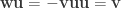
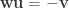
Lo and behold, these are the exact same relations that hold among 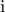 ,
, 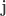 , and
, and  and that are used to define the quaternions! In other words, it turns out that we have made a copy of the quaternions using
and that are used to define the quaternions! In other words, it turns out that we have made a copy of the quaternions using 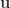 ,
, 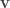 , and
, and 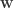 in place of
in place of 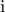 ,
, 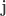 , and
, and  . This is an automorphism of the quaternions.
. This is an automorphism of the quaternions.
What makes this automorphism work? Well, it is essential that 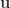 ,
, 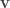 , and
, and 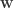 be mutually orthogonal and that each of them have length
be mutually orthogonal and that each of them have length  . But this is not all, they must also have the correct orientation. For example,
. But this is not all, they must also have the correct orientation. For example, 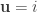 ,
,  ,
, 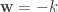 would not work. The automorphisms of the quaternions are therefore exactly the proper rotations of
would not work. The automorphisms of the quaternions are therefore exactly the proper rotations of 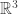 .
.
Now what happens to all the quaternions when we multiply them on the left by a unit vector 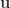 ? To answer this, let’s first construct
? To answer this, let’s first construct 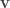 and
and 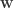 as we did above. We let
as we did above. We let 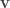 be any unit vector orthogonal to
be any unit vector orthogonal to 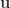 , and we let
, and we let  . Now any quaternion can be expressed as a linear combination of
. Now any quaternion can be expressed as a linear combination of  ,
, 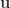 ,
, 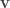 , and
, and 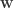 , and this is more convenient for our purposes than the conventional expression of a quaternion as a linear combinations of
, and this is more convenient for our purposes than the conventional expression of a quaternion as a linear combinations of  ,
, 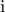 ,
, 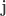 , and
, and  . So:
. So:

What happened? Well, we simultaneously rotated by  degrees in the
degrees in the 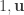 -plane and in the
-plane and in the  -plane. This is called a double rotation, and it is not possible in 3 dimensional space because it requires two orthogonal planes. Here is a projection onto 3-space of a 4-dimensional hypercube undergoing a double rotation.
-plane. This is called a double rotation, and it is not possible in 3 dimensional space because it requires two orthogonal planes. Here is a projection onto 3-space of a 4-dimensional hypercube undergoing a double rotation.

It is simultaneously rotating and turning inside out. The turning inside out, however, is really a projection of a rotation in an orthogonal plane. The small cube in the center is not really smaller than the cube around it, it is just further away from the viewer. As the hypercube turns inside out, each constituent cube comes closer and goes farther away.
Now let’s take the general case of multiplying quaternions on the left by a unit quaternion  . For a quaternion
. For a quaternion  , we get
, we get
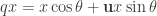
This is a linear combination of  and
and 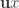 ,
,  doubly rotated by 90 degrees. When we combine these two things this way, we end up rotating
doubly rotated by 90 degrees. When we combine these two things this way, we end up rotating  by
by  . Indeed, if
. Indeed, if 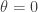 then
then  and if
and if  then
then  . If you think about this you’ll see that as
. If you think about this you’ll see that as  increases
increases  doubly rotates by the angle
doubly rotates by the angle  in the
in the 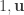 -plane and in the
-plane and in the  -plane.
-plane.
It is important to note that  rotates at the same rate in both planes. A double rotation where both rotations are of the same angle is called an isoclinic rotation.
rotates at the same rate in both planes. A double rotation where both rotations are of the same angle is called an isoclinic rotation.
Now what about multiplying quaternions on the right by a unit quaternion  ? Quaternions aren’t commutative right, so maybe it will do something different? Well it does! First let’s just multiply on the right by
? Quaternions aren’t commutative right, so maybe it will do something different? Well it does! First let’s just multiply on the right by 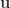 :
:
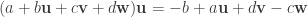
This is just like the multiplying on the left except the signs of the 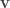 and
and 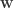 terms have flipped. It is a double rotation again, but now we are rotating the planes opposite ways. The general case works as expected:
terms have flipped. It is a double rotation again, but now we are rotating the planes opposite ways. The general case works as expected:

So we doubly rotate  by the angle
by the angle  in the
in the 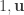 -plane and by the angle
-plane and by the angle 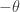 in the
in the  -plane.
-plane.
We distinguish isoclinic rotations by whether they rotate the planes in the same or opposite directions. If they rotate the planes in the same direction, they are called left isoclinic rotations, and if opposite, they are called right isoclinic rotations. Left isoclinic rotations have come about through left quaternion multiplication, and right one have come about through right quaternion multiplication, but is it possible to do the reverse? No. Every left multiplication yields a left isoclinic rotation, as we have seen, and a left isoclinic rotation can’t also be a right one. This is related to the previous point that 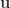 ,
, 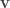 , and
, and 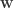 must have the same orientation as
must have the same orientation as 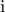 ,
, 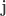 , and
, and  .
.
Now, finally, let’s justify the claim above. What happens to a quaternion  when we left-multiply it by
when we left-multiply it by  and right-multiply it by
and right-multiply it by 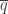 ? If
? If  , then
, then  . Thus the two isoclinic rotations performed on
. Thus the two isoclinic rotations performed on  are in the same planes and by the same angle but they are in different directions. Also, one of them is left and one is right. Let’s write down what they do:
are in the same planes and by the same angle but they are in different directions. Also, one of them is left and one is right. Let’s write down what they do:
Left-multiplication by  : Rotates by
: Rotates by  in the
in the 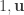 -plane and by
-plane and by  in the
in the  -plane.
-plane.
Right-multiplication by 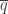 : Rotates by
: Rotates by 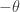 in the
in the 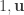 -plane and by
-plane and by  in the
in the  -plane.
-plane.
So the combined effect is to rotate by  in the
in the 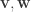 -plane and do nothing else! Since we don’t touch the real component of
-plane and do nothing else! Since we don’t touch the real component of  , we are then rotating
, we are then rotating 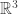 exclusively. Since we don’t touch the
exclusively. Since we don’t touch the  -component of
-component of  , the vector
, the vector  must be our axis of rotation. Thus we did it! This is why conjugation by
must be our axis of rotation. Thus we did it! This is why conjugation by  is rotation by angle
is rotation by angle  about
about  !
!
Before I go, here’s some more cool stuff about this. Notice the factor of  . This is interesting because it means that if
. This is interesting because it means that if 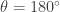 we won’t rotate at all. In this case,
we won’t rotate at all. In this case, 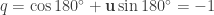 . So the unit quaternions
. So the unit quaternions  and
and 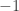 both correspond to not rotating at all. These are actually the only such unit quaternions, because every other unit quaternion has an angle
both correspond to not rotating at all. These are actually the only such unit quaternions, because every other unit quaternion has an angle  such that
such that  . More generally, there are exactly two unit quaternions that correspond to any rotation:
. More generally, there are exactly two unit quaternions that correspond to any rotation:  and
and  . This means that the 3-sphere of unit quaternions is a double cover of the space of proper rotations of 3-space. This fact was exploited in the very cool game Hypernom.
. This means that the 3-sphere of unit quaternions is a double cover of the space of proper rotations of 3-space. This fact was exploited in the very cool game Hypernom.
Also, I’d like to mention rotations in the 4-space that quaternions live in. We know how to do left and right isoclinic rotations in this space, but how do we do general rotations? Well, it turns out we can put together a left and a right isoclinic rotation to do any rotation we want. This can be written  , where
, where  and
and  are unit quaternions which are performing left and right isoclinic rotations on
are unit quaternions which are performing left and right isoclinic rotations on  respectively. I’ll show how to make any single rotation, and you can put these together to make double rotations (not necessarily isoclinic).
respectively. I’ll show how to make any single rotation, and you can put these together to make double rotations (not necessarily isoclinic).
Let’s say we want to rotate by the angle  in the plane spanned by quaternions
in the plane spanned by quaternions  and
and  . If
. If  and
and  are both fully imaginary, we already know how to do this. So let’s consider the case wherein
are both fully imaginary, we already know how to do this. So let’s consider the case wherein  has non-zero real component. If
has non-zero real component. If 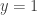 , then
, then  must be fully imaginary. We then follow a procedure very similar to the previous. We do a left and a right isoclinic rotation, both of which rotate in the same direction by
must be fully imaginary. We then follow a procedure very similar to the previous. We do a left and a right isoclinic rotation, both of which rotate in the same direction by  in the
in the 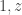 plane and which cancel in the orthogonal plane. This can be written
plane and which cancel in the orthogonal plane. This can be written  . Notice the absence of the conjugate.
. Notice the absence of the conjugate.
Now if 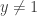 , but still has non-zero real component, we can turn it to be
, but still has non-zero real component, we can turn it to be  , perform the rotation in the way just described, and then turn it back. In more detail:
, perform the rotation in the way just described, and then turn it back. In more detail:
Step 1. Singly rotate in the  -plane so that
-plane so that  maps to
maps to  . Let
. Let 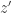 be the rotated version of
be the rotated version of  .
.
Step 2. Rotate in the  -plane by
-plane by  .
.
Step 3. Perform the same rotation as step 1 but in reverse.
Now, I claimed that every rotation could be written as  , but now we have multiple steps. What’s going on? Well, we can write each step this way. Step 1 can be written
, but now we have multiple steps. What’s going on? Well, we can write each step this way. Step 1 can be written 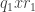 , step 2
, step 2  , and step 3 is just the inverse of step 1:
, and step 3 is just the inverse of step 1:  . Doing all these steps sequentially yields
. Doing all these steps sequentially yields 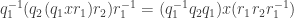 . This is of the required form because
. This is of the required form because  and
and  are both unit quaternions performing left and right isoclinic rotations on
are both unit quaternions performing left and right isoclinic rotations on  respectively.
respectively.
So every rotation in 4-space can be accomplished with two unit quaternions,  and
and  . Rotating a quaternion
. Rotating a quaternion  then yields
then yields  . This means that rotations in 4-space can be represented by pairs of quaternions. However, just like in the case of rotations in 3-space, there are actually exactly two pairs of quaternions corresponding to every 4-spatial rotation:
. This means that rotations in 4-space can be represented by pairs of quaternions. However, just like in the case of rotations in 3-space, there are actually exactly two pairs of quaternions corresponding to every 4-spatial rotation:  and
and  . We can see this because
. We can see this because 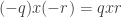 . But why are these the only two? Well, suppose that we had another pair
. But why are these the only two? Well, suppose that we had another pair 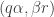 . Then
. Then  , which simplies to
, which simplies to  . This must hold for all
. This must hold for all  , so we can choose
, so we can choose 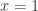 in particular, to attain
in particular, to attain 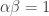 . This means that
. This means that 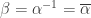 , so
, so  is a rotation of
is a rotation of 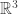 . Since it doesn’t change anything,
. Since it doesn’t change anything, 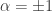 .
.